Atomic, Molecular, and Optical Physics

 

1. Many-Body Excitations in Trapped Bose-Einstein Condensates

Excitation spectra of quantum systems are one of the widely used notions in our modern quantum world. They often allow one to explore the microscopic structure of different quantum objects, such as nuclei, atoms, molecules, and solids, and more recently, of Bose-Einstein condensates (BECs). Experimentally, owing to their controllability, excitations of BECs have widely been explored. Theoretically, excitation spectra of dilute BECs have amply been studied within Bogoliubov—de Gennes theory, which assumes the presence of a simple condensate and only a small amount of excitations and quantum depletion atop.

There are available experiments with BECs which have measured and identified excitations that cannot be described by the standard Bogoliubov—de Gennes theory. Our group develops and utilizes novel theoretical and computational methods, noticeably the multiconfigurational time-dependent Hartree for bosons (MCTDHB) method and its linear-response (LR-MCTDHB) atop, to describe and investigate such excitations. 

2. Many-body Tunneling Processes of Bose-Einstein Condensates

Tunneling is a process which lies at the very heart of quantum mechanics. It is of general and wide interest and of importance in physics, chemistry, biology, and technology. Already the text-book example of single-particle tunneling under a potential barrier in one spatial dimension is wealth. Interactions between tunneling particles make it profoundly richer. Higher spatial dimensions open essentially unlimited possibilities.

Bose-Einstein condensates offer the opportunity to theoretically study tunneling processes in a synthetic yet highly controllable many-particle system. Our group investigates how interactions, trapping, topology, and dimensionality conspire to allow for novel many-particle tunneling phenomena and mechanisms in BECs, with core emphasis on the time-dependent description of the tunneling process.

3. Variance as a Sensitive Probe of Correlations in Interacting Bose Systems

Bose-Einstein condensates made of ultra-cold trapped bosonic atoms have become a central venue in which interacting many-body quantum systems are studied. The ground state of a trapped BEC has been proven to be 100% condensed in the limit of an infinite number of particles and at constant interaction parameter, i.e., when the product of the number of particles times the scattering length is fixed. The meaning of this result is that properties of the condensate, noticeably its energy per particle and density per particle, converge to those obtained by minimizing the Gross-Pitaevskii, mean-field energy functional. This naturally raises the question whether correlations are of any importance in this limit.

Our group explores, numerically and analytically, the variance of many-particle operators which can show, even in the infinite-particle limit and at constant interaction parameter, substantial deviation from the Gross-Pitaevskii, mean-field result, thus elucidating the presence of many-body correlations in this limit.

4. Solvable Many-Body Models of Bose-Einstein Condensates and Mixtures Thereof

Solvable many-body models offer the unique possibility to investigate quantum many-particles systems analytically. They can provide definite answers on questions arising from preliminary intuition, and complement investigations necessitating numerical tools. In the latter context, solvable many-body models are also instrumental in benchmarking numerical methods.

Our group develops and applies solvable models, chiefly by generalizing the harmonic-interaction model for mixtures of identical particles, to investigate fundamental properties of trapped mixtures at the inter-junction of many-body and Gross-Pitaevskii, mean-field physics, such as the energy, density and reduced density matrices, separability, variance, and uncertainty product. 

 

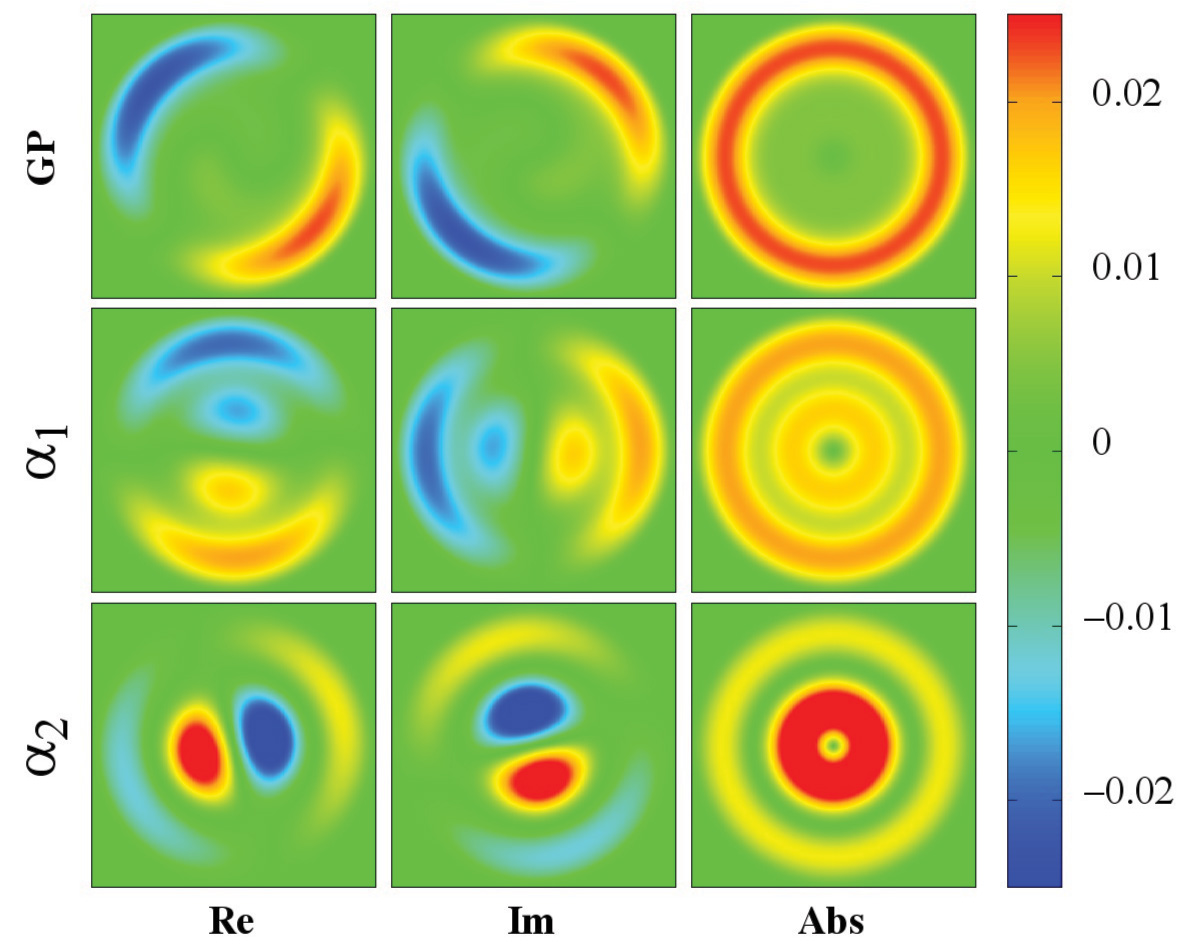
Figure 1: Tunneling and fragmentation of a BEC vortex in a circular trap. For more details see Phys. Rev. A 92, 043627 (2015). [LINK TO: https://doi.org/10.1103/PhysRevA.92.043627]

 

 

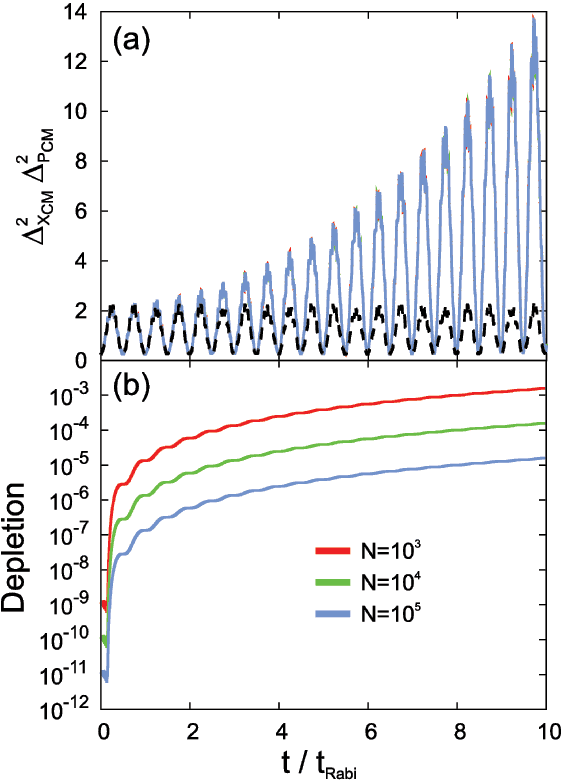
Figure 2: Center-of-mass uncertainty product of a BEC in a bosonic Josephson junction. For more details see Phys. Rev. A 93, 023605 (2016). [LINK TO: https://doi.org/10.1103/PhysRevA.93.023605]

 

 

 

 

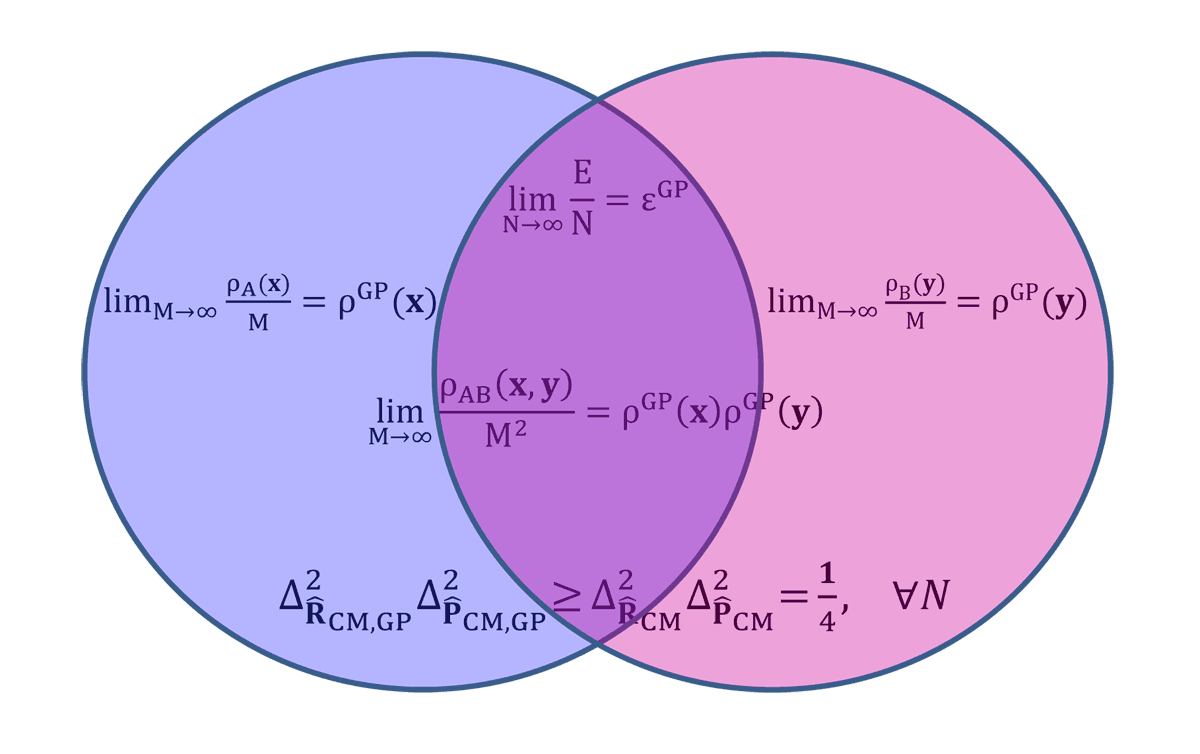
Figure 3: An artist’s view of variance in a trapped BEC mixture at the infinite-particle limit. For more details see Chem. Phys. 482, 362 (2017). [LINK TO: http://dx.doi.org/10.1016/j.chemphys.2016.07.011]